Problem arose from BME - Medical Robotics - 2 - Spatial Descriptions - Slides

-
First, why do minuses appear? From a mathematical point of view, rotation matrices are skew-symmetric, i.e. \(R^T = R^{-1}\). \(R^{-1}\) equals replace \(\theta\) with \(-\theta\) So it is not possible to define a rotation matrix without minuses or zeros appearing on non-diagonal elements.
- And the convention of these rotation matrices follow the same positive direction of rotation as the cross product in a right handed coordinate system.
- See the picture below
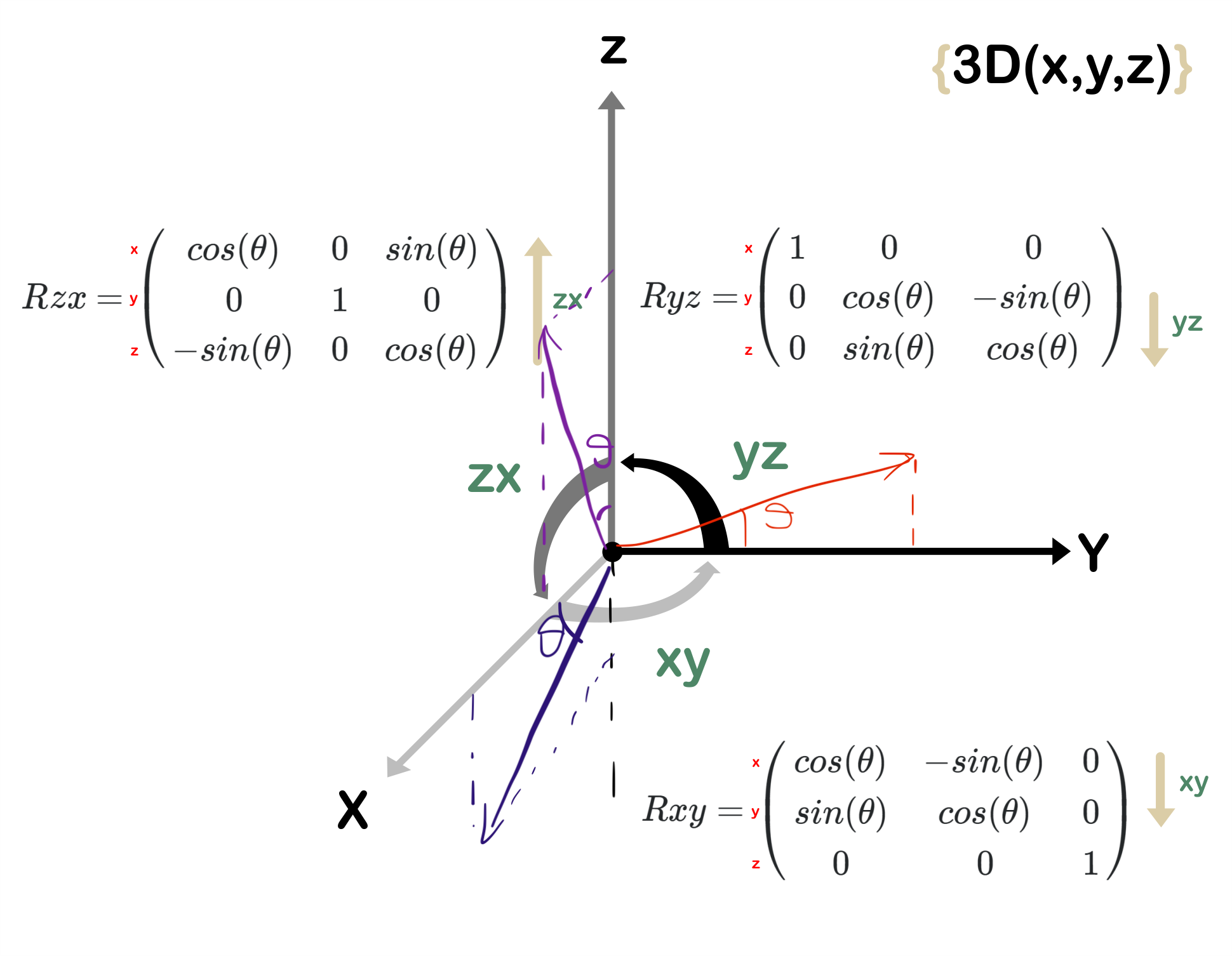
- when considering the rotation in YZ plane along x-axis, original unit vector along y is mapped to the red vector i drew. It is easy to see the coordinate for it is \([0, cos(\theta), sin(\theta)]^T\). However, if we look at the rotation in ZX plan along y-axis, the original unit vector along x-axis is mapped to the dark-blue vector and its coordinates is \([cos(\theta), 0, -sin(\theta)]^T\), and the unit vector along z-axis is mapped to the purple vector whose coordinates is \([sin(\theta), 0, cos(\theta)]^T\). Therefore we get the whole \(R_{zx}\) matrix.
- Another way of thinking is that just look at the axis, a 90° rotation around the x-axis maps the y-axis to the positive z-axis and the z-axis to the negative y-axis; a 90° rotation around the y-axis maps the z-axis to the positive x-axis and the x-axis to the negative z-axis; a 90° rotation around the z-axis maps the x-axis to the positive y-axis and the y-axis to the negative x-axis.
This explains why the rotation along y-axis looks clockwise while the rotation along x and z-axis are counterclockwise.